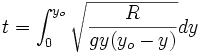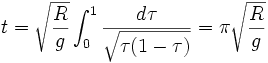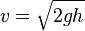La cycloïde

La cycloïde

Introduction
Définition
Propriétés et applications
Essentielle dans l'étude de l'isochronisme des oscillations
Une courbe brachistochrone
Pour aller un peu plus loin

Introduction

Nous montrons en Seconde que le mouvement d'un système ponctuel dépend du point d'observation ou, plus précisément, du référentiel d'étude. Si la trajectoire de la valve d'une roue de vélo est bien un cercle dans un référentiel attaché au cadre du vélo, sa trajectoire est plus complexe dans un référentiel terrestre attaché à la route.

Le point mobile engendre une cycloïde droite

La courbe étrange formée est appelée cycloïde droite. En mathématiques, la cycloïde droite, aussi appelée roue d'Aristote ou roulette de Pascal, est une courbe plane transcendante, trajectoire d'un point fixé à un cercle qui roule sans glisser sur une droite. Il s'agit donc d'une courbe cycloïdale dont la directrice est une droite et dont le point directeur est situé sur le cercle lui-même; c'est un cas particulier de ce que les mathématiciens appellent "roulette".

Remarque : La cycloïde peut aussi être observée par le fait qu'étant donné deux droites parallèles, les deux points I et N d'intersection de la tangente et de la normale avec ces deux droites sont tels que la droite (IN) reste orthogonale à ces deux droites.

Le mot "cycloïde" vient du grec kuklos (cercle, roue) et eidos (forme, semblable à), bien que cette courbe n'ait pas été connue des Grecs et ne fut baptisée ainsi qu'en 1599 par Galilée.

Elle fut étudiée pour la première fois au XV^e siècle par Nicolas de Cues alors qu'il essayait de déterminer la surface du cercle par intégration. En 1626, Mersenne en reprit l'étude et essaya, sans succès, de déterminer l'aire sous une arche de cycloïde. Il faudra attendre 1634 pour que son confrère Roberval démontre que cette aire est égale à trois fois l'aire du cercle qui l'a générée.

Descartes, qui fut consulté sur ce calcul, le trouva intéressant mais trivial. Galilée, pour sa part, avait étudié ce problème pendant quarante ans mais n'était arrivé au même ratio que par une méthode empirique mettant en jeu des mesures de poids ; il crut d'ailleurs que ce ratio n'était pas entier.

La cycloïde et le calcul de ses propriétés furent alors l'objet de défis constants entre mathématiciens, si bien qu'elle fut surnommée « l'Hélène des géomètres ». Après Descartes, Pascal (sous le pseudonyme de Dettonville) offrit un prix à qui résoudrait deux problèmes liés à la cycloïde et au mouvement du pendule. En 1658, Christopher Wren démontra que la longueur d'une arche de cycloïde est égale à quatre fois le diamètre du cercle qui l'a générée. En 1673, Christiaan Huygens l'évoqua dans un traité sur le pendule synchrone.

Pendule de Huygens

Enfin, ses propriétés brachistochrones furent étudiées à partir de 1696 par Jean Bernoulli, puis par Isaac Newton, Leibniz, Jacques Bernoulli et L'Hôpital. Il s'agissait d'un des premiers problèmes de variations, et son étude fut le point de départ de l'élaboration du calcul des variations.

Définition

La cycloïde droite peut être définie paramétriquement par le système suivant.

En savoir plus sur ces équations : http://www.mathcurve.com/courbes2d/base/base.shtml

L'équation cartésienne est de la forme

On peut aussi la définir dans l'espace complexe

ou comme une solution de l'équation différentielle

Il existe enfin des équations intrinsèques du type

où le rayon de courbure RC et l'abscisse curviligne s sont par exemple définis par

Propriétés et applications

Une arche de cycloïde a une longueur de 8 R et une aire de 3π R².

La roulette de la pointe d'une cardioïde roulant sur une cycloïde de même longueur est rectiligne.

La trajectoire d'une particule de masse m et de charge q soumise sans vitesse initiale à un champ électrique et un champ magnétique orthogonaux uniformes d'intensités E et B est une cycloïde orthogonale au champ magnétique :

avec

Essentielle dans l'étude de l'isochronisme des oscillations

La courbe isochrone de Huygens est la courbe telle qu'un point matériel se déplaçant sans frottement sur elle a un mouvement périodique dont la période est indépendante de la position initiale ; la solution est une arche de cycloïde dont les points de rebroussement sont situés vers le haut ; l'isochronie vient en fait de la tautochronie. La période du mouvement est

où L est la flèche de la cycloïde.

Le pendule cycloïdal de Huygens ci-dessous utilise cette propriété et le fait que la développée (ou caustique, focale : lieu des centres de courbure, ou encore enveloppe des normales) d'une cycloïde est une cycloïde égale. Son intérêt est d'avoir une période d'oscillation (cf. ci-dessus) indépendante de l'amplitude, contrairement au pendule libre dont seules les "petites" oscillations peuvent être considérées comme ayant la période T.

Dans ce problème de Huygens, tous les points atteignent le point le plus bas en même temps ; Galilée a posé le même problème, mais pour des points matériels se déplaçant sur des supports rectilignes.

L’équation différentielle décrivant la cycloïde générée par un cercle de rayon R, est:

$\begin{pmatrix}\frac{dy}{dx}\end{pmatrix}^2=\frac{2R-y}{y}$

Pour l’exercice qui nous intéresse on utilise une cycloïde inversée (tête en bas) dont l’équation différentielle prend la forme

$\begin{pmatrix}\frac{dy}{dx}\end{pmatrix}^2=\frac{y}{2R-y}$

On place une particule sur la courbe à la position de coordonnées $(x o, y o)$ et on laisse la gravité agir (constante gravitationnelle g). La vitesse en un point quelconque (x, y) de la courbe est

$v=\sqrt{2g(y_o-y)}$

Le temps pris par la particule pour effectuer le trajet infinitésimal jusqu’au point de la courbe (x+dx, y+dy) est

$dt=\frac{\sqrt{dx^2+dy^2}}{\sqrt{2g(y_o-y)}}=\sqrt{\frac{R}{gy(y_o-y)}}dy$

Le temps t que prendra la particule pour arriver au bas de la cycloïde est

$t=\int_0^{y_o}{\sqrt{\frac{R}{gy(y_o-y)}}dy}$

En effectuant le changement de variable

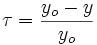
$\tau=\frac{y_o-y}{y_o}$

on trouve

$t=\sqrt{\frac{R}{g}}\int_0^1{\frac{d\tau}{\sqrt{\tau(1-\tau)}}}=\pi\sqrt{\frac{R}{g}}$

d’où il ressort que le temps de trajet est indépendant du point de départ sur la cycloïde.

Une courbe brachistochrone

C'est une courbe brachistochrone ("brakhisto" signifiant "le plus court") au sens de Roberval, c'est-à-dire qu'une cycloïde représente la courbe sur laquelle doit glisser sans frottement et sans vitesse initiale, un point matériel pesant placé dans un champ de pesanteur uniforme de sorte que son temps de parcours soit minimal parmi toutes les courbes joignant deux points fixés. Autrement dit, c'est la courbe de descente la plus rapide pour aller d'un point A à un point B.

Une courbe brachistochrone est une courbe sur laquelle doit glisser sans frottement et sans vitesse initiale, un point matériel pesant placé dans un champ de pesanteur uniforme de sorte que le temps de parcours soit minimal parmi toutes les courbes joignant deux points O et A fixés (ici A(a, -b)).

Réponse pour a > 0 (résultat trouvé en même temps par Leibniz, Newton, L'Hospital, Jean et Jacques Bernoulli) : un arc de cycloïde commençant avec une tangente verticale.

Il est remarquable que si la pente b/a entre O et A est inférieure à 2/p » 63%, correspondant à un angle de »32 ° avec l'horizontale, la courbe la plus rapide possède, comme dans la figure ci-dessus, une portion qui remonte !

Ceci vaut à la limite si les points O et A sont à la même altitude, auquel cas la ligne droite donnerait un temps de parcours infini.
Pour a = b = 1 m, on trouve un temps de descente de 0,58 s pour la cycloïde, de

pour un arc de cercle, de

pour la ligne droite, et

pour une chute libre suivie d'un parcours horizontal (qui est donc battu par la ligne droite).

La résolution du problème de la courbe brachistochrone passionna les mathématiciens. Isaac Newton fut mis au défi de le résoudre en 1696 et y serait parvenu en seulement une journée. En fait, la solution fut découverte en même temps par Leibniz, Newton, L'Hôpital, Jean et Jacques Bernoulli : il s'agit d'un arc de cycloïde commençant avec une tangente verticale.

Le chemin le plus court entre deux points est celui que suivrait un rayon de lumière. La courbe brachistochrone est donc simplement le trajet suivi par la lumière dans un milieu ou la vitesse augmente selon une accélération constante (l’attraction terrestre g). La loi de la conservation de l’énergie permet d’exprimer la vitesse d’un corps soumis à l’attraction terrestre par

$v=\sqrt{2gh}$

où h représente la perte d’altitude par rapport au point de départ. Il est à noter que la vitesse ne dépend pas du départ horizontal.

La loi de la réfraction indique que tout au long de sa trajectoire un rayon lumineux obéit à la règle

$\frac{\sin{\theta}}{v}=Cste$

où $θ$ représente l’angle par rapport à la verticale. En insérant dans cette formule l’expression de la vitesse trouvée plus haut, on constate immédiatement deux choses:

1- Au point de départ, lorsque la vitesse est nulle, l’angle doit nécessairement être nul. Donc la courbe brachistochrone est tangente à la verticale à l’origine.

2- La vitesse est bornée car le sinus ne peut être supérieur à 1. Cette vitesse maximum est atteinte quand la particule (ou le rayon) passe par l’horizontale (ce « passage » pouvant être asymptotique.)

Sans restreindre la généralité du problème, on va supposer que la particule part du point de coordonnées (0,0) et que la vitesse maximum est atteinte à l’altitude –D. La loi de la réfraction s’exprime alors par

$\frac{\sin{\theta}}{\sqrt{-2gy}}=\frac{1}{\sqrt{2gD}}$

Sachant que la particule se déplace sur une courbe, on a la relation :

$\sin{\theta}=\frac{dx}{\sqrt{dx^2+dy^2}}$

En insérant cette expression dans la formule précédente et en réarrangeant les termes on trouve

$\begin{pmatrix}\frac{dy}{dx}\end{pmatrix}^2=-\frac{D+y}{y}$

ce qui est l’équation différentielle de l’opposée d’une cycloïde, générée par un cercle de diamètre D.

La calcul des variations a amené une autre démonstration.

On note $C (t) = (x (t), y (t))$ la courbe recherchée, paramétrée par $t$ . L'équation cartésienne est $y = f (x)$ (on exclut les courbes ayant des parties verticales). On exprime un déplacement infinitesimal sur la courbe

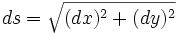
$ds = \sqrt{(dx)^2 + (dy)^2}$

Si on pose que la dérivée de la courbe est

$y'=\frac{\partial y(t)}{\partial x(t))}$

on a

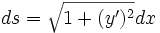
$ds = \sqrt{1 + (y')^2}dx$

Mais, d'autre part, on a toujours, en vertu du théorème de l'énergie cinétique, la relation suivante:

$v = \frac{ds}{dt} = \sqrt{2gy}$

On peut alors exprimer le temps de parcours infinitésimal $dt$

$dt = \sqrt{\frac{1+{y'}^2}{2gy}} dx$

Donc

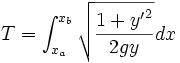
$T = \int_{x_a}^{x_b}\sqrt{\frac{1+{y'}^2}{2gy}} dx$

Avec T le temps de parcours (à minimiser), $x a$ et $x b$ les abscisses de départ et d'arrivée.

Il s'agit donc de trouver le minimum de la fonctionnelle

$F : y\mapsto \int_{x_a}^{x_b}\sqrt{\frac{1+{y'}^2}{2gy}} dx$

Les points critiques d'une telle fonctionnelle sont donnés par l'équation d'Euler-Lagrange. Après calcul et simplification, on obtient que $y$ est un point critique de $F$ si :

$\frac{1}{\sqrt{2gy} \sqrt{1 + {y'}^2}}=C$

On obtient donc l'équation différentielle

$\left[ 1 + {y'}^2 \right] y = k^2$

Pour résoudre l'équation, on procède au changement de variable suivant

$y'= \operatorname{cotan}\left( \frac{\theta}{2} \right)$

Dans ce cas, on obtient l'équation paramétrique de la courbe solution

$x(\theta) = k\left(\theta - \sin(\theta)\right)$

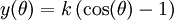
$y(\theta) = k\left(\cos(\theta) -1\right)$

Il s'agit de la cycloïde sous sa forme paramétrée.

Pour aller plus loin

Cycloïde, hypocycloïde et épicycloïde : http://www.univ-lemans.fr/enseignements/physique/02/meca/cyclo.html
La trajectoire de Mars dans le référentiel géocentrique, comme nous l'avons montré en TP de Seconde, est épicycloïde.